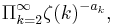Hafner–Sarnak–McCurley constant
The Hafner-Sarnak-McCurley constant is a mathematical constant representing the probability that the determinants of two randomly chosen square integer matrices will be relatively prime. The probability depends on the matrix size, n, in accordance with the formula
![D(n)=\Pi_{k=1}^{\infty}\left\{1-[1-\Pi_{j=1}^n(1-p_k^{-j})]^2\right\},](/2012-wikipedia_en_all_nopic_01_2012/I/d0713330124f8206dbdc8bd6ce32b2c4.png)
where pk is the kth prime number. The constant is the limit of this expression as n approaches infinity. Its value is roughly 0.3532363719... (sequence A085849 in OEIS); Ilan Vardi has given it the alternate expression
which converges exponentially; here ζ(k) is the Riemann zeta function.
References
- Finch, S. R. (2003), "§2.5 Hafner-Sarnak-McCurley Constant", Mathematical Constants, Cambridge, England: Cambridge University Press, pp. 110–112, ISBN 0521818052.
- Flajolet, I. & Vardi (1996), "Zeta Function Expansions of Classical Constants", Unpublished manuscript, http://algo.inria.fr/flajolet/Publications/landau.ps.
- Hafner, J. L.; Sarnak, P. & McCurley, K. (1993), "Relatively Prime Values of Polynomials", in Knopp, M. & Seingorn, M., A Tribute to Emil Grosswald: Number Theory and Related Analysis, Providence, RI: Amer. Math. Soc., ISBN 0821851551.
- Vardi, I. (1991), Computational Recreations in Mathematica, Redwood City, CA: Addison-Wesley, ISBN 0201529890.